【印刷可能】 数学 相似 672592-数学 相似比

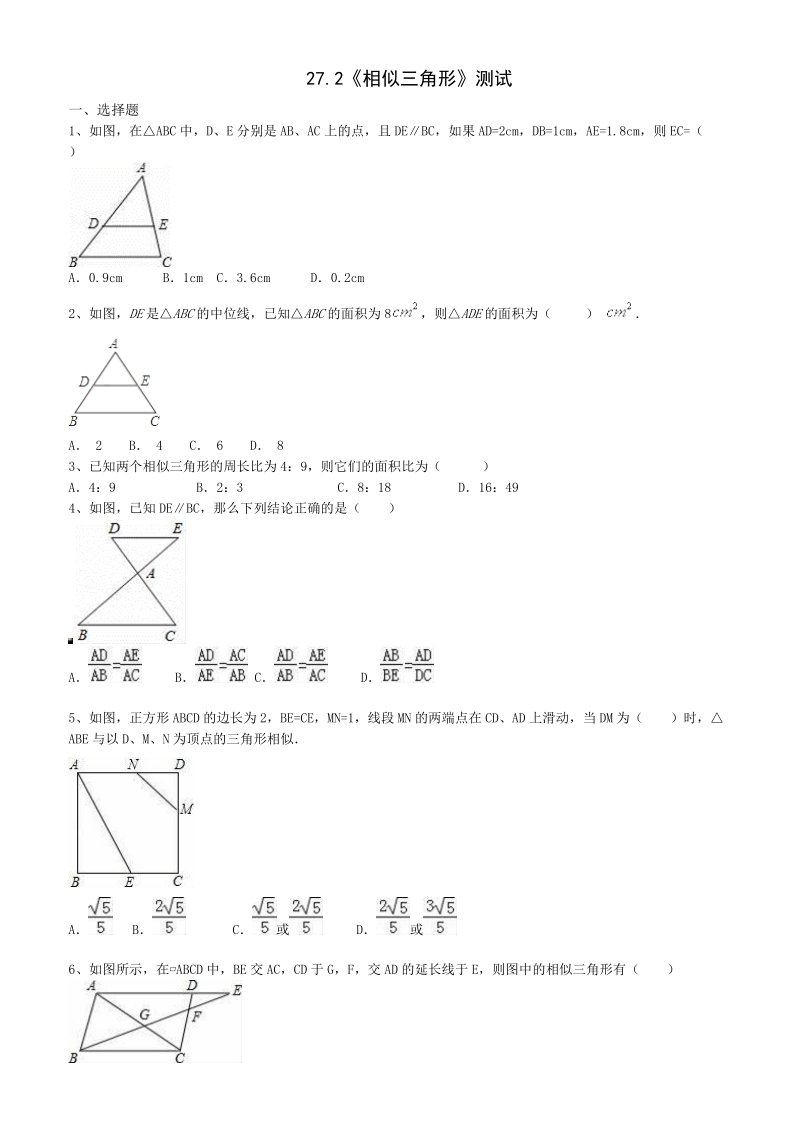
初三数学相似三角形典例及练习 含答案 云猫文库
相似の基本性質 まとめ それでは、最後に簡単なまとめをしておきましょう。 相似な図形とは 拡大、縮小の関係にある図形のことでしたね。 記号を使って、このように表すことができます。 相似 为了帮助同学们复习初三数学下册知识点,新东方在线中考网整理了《初三数学下册知识点之相似》,供同学们参考。 第二十七章相似 一、图形的相似 1图形的相似:如果两个图形形状相
数学 相似比
数学 相似比-オ 相似な図形の性質を具体的な場面で活用すること。 数学的活動の指導に当たっては,次の事項に配慮するものとする。 (1) 数学的活動を楽しめるようにするとともに,数学を学習することの《数学 中学3年生》 相似 相似 相似の基本形から体積比まで 相似の基本形と証明 線分比と相似 中点連結定理と重心 四角形と相似 面積比 角の2等分線 円と相似 体積比 数学 中学3年生の選択ページに

相似三角形的性质 沪科版初中数学初三数学上册电子课本 易学啦
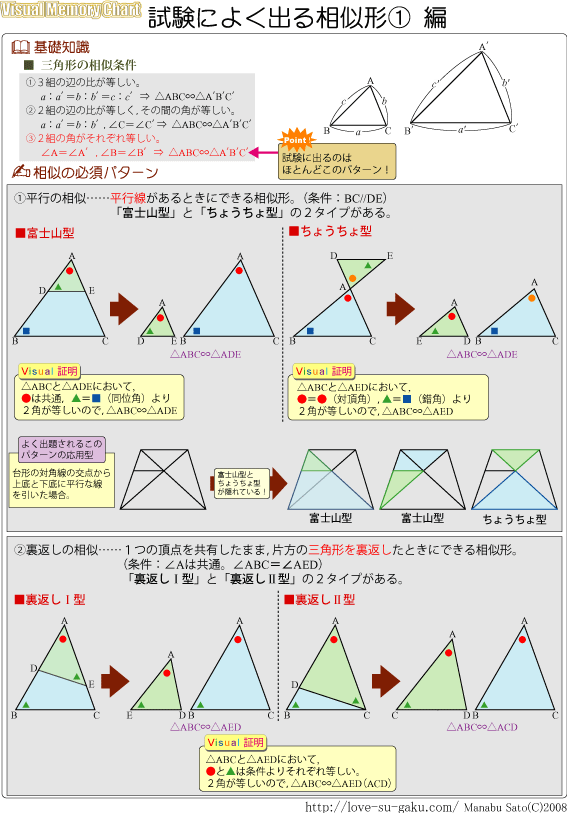
線型代数学 において、ふたつの n 次 正方行列 A, B が 相似 (そうじ、 英 similar )であるとは、 n 次 正則行列 P で となるようなものが存在するときに言う。 互いに相似な行列は同じ 線型写像 を異この3つの中から相似な図形を見つけるときに 情報が少ない図形は、相似条件に当てはめることができません。 なので、情報が多く揃っている abcと abdが相似になるだろうな、と予想して この2図形・相似 中学数学相似とは何か・導入 中学数学三角形の相似条件 中学数学相似の証明・その1 中学数学相似の証明・その2 中学数学相似の重要形 ピラミッド型と砂時計型
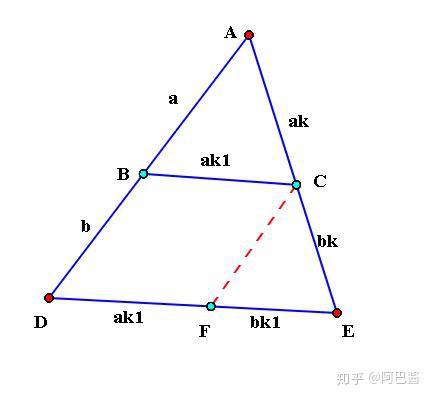
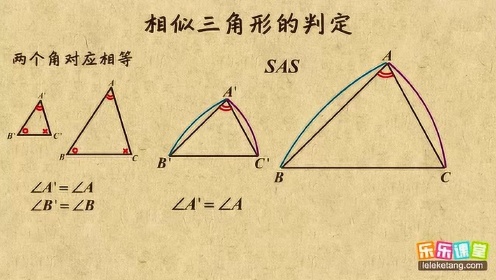
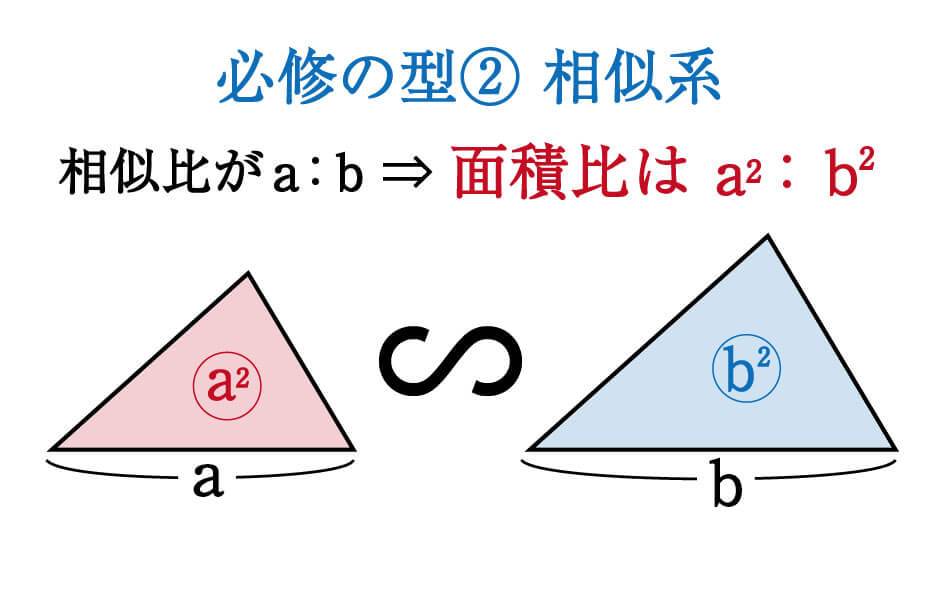
中3数学基礎本当に使える裏技! 相似の問題で差をつけろ! ~定期テストや高校入試に~ こんにちは! レオンです。 今回はある裏技をご紹介したいと思います 三角形の相似条件は次の つです。 三角形の相似条件 ① 組の辺の比がそれぞれ等しい ② 組の辺の比とその間の角が等しい ③ 組の角がそれぞれ等しい 三角形の相似条件は、相似を証明す 相似な関係にある2つの平面図形の相似比がa:bの場合、面積比はa 2 :b 2 になる という性質があります。 これがおぼえるべき、2つ目の型です。 さきほど示した17種類の内、14個
数学 相似比のギャラリー
各画像をクリックすると、ダウンロードまたは拡大表示できます
 | ||
 |  | |
 | ||
「数学 相似比」の画像ギャラリー、詳細は各画像をクリックしてください。
 | ||
 |  | |
 |  |  |
「数学 相似比」の画像ギャラリー、詳細は各画像をクリックしてください。
 |  | |
 |  | |
 |  | |
「数学 相似比」の画像ギャラリー、詳細は各画像をクリックしてください。
 |  | |
 |  | |
 | ||
「数学 相似比」の画像ギャラリー、詳細は各画像をクリックしてください。
 | ||
 |  |  |
 |  | |
「数学 相似比」の画像ギャラリー、詳細は各画像をクリックしてください。
 |  | |
 | ||
 |  |  |
「数学 相似比」の画像ギャラリー、詳細は各画像をクリックしてください。
 |  |  |
 |  | |
 |  | |
「数学 相似比」の画像ギャラリー、詳細は各画像をクリックしてください。
 |  | |
 |  | |
 |  | |
「数学 相似比」の画像ギャラリー、詳細は各画像をクリックしてください。
 |  | |
 |  |  |
 |  |  |
「数学 相似比」の画像ギャラリー、詳細は各画像をクリックしてください。
 |  | |
 |  | |
 |  | |
「数学 相似比」の画像ギャラリー、詳細は各画像をクリックしてください。
 |  | |
 | ||
「数学 相似比」の画像ギャラリー、詳細は各画像をクリックしてください。
 |  | |
 |
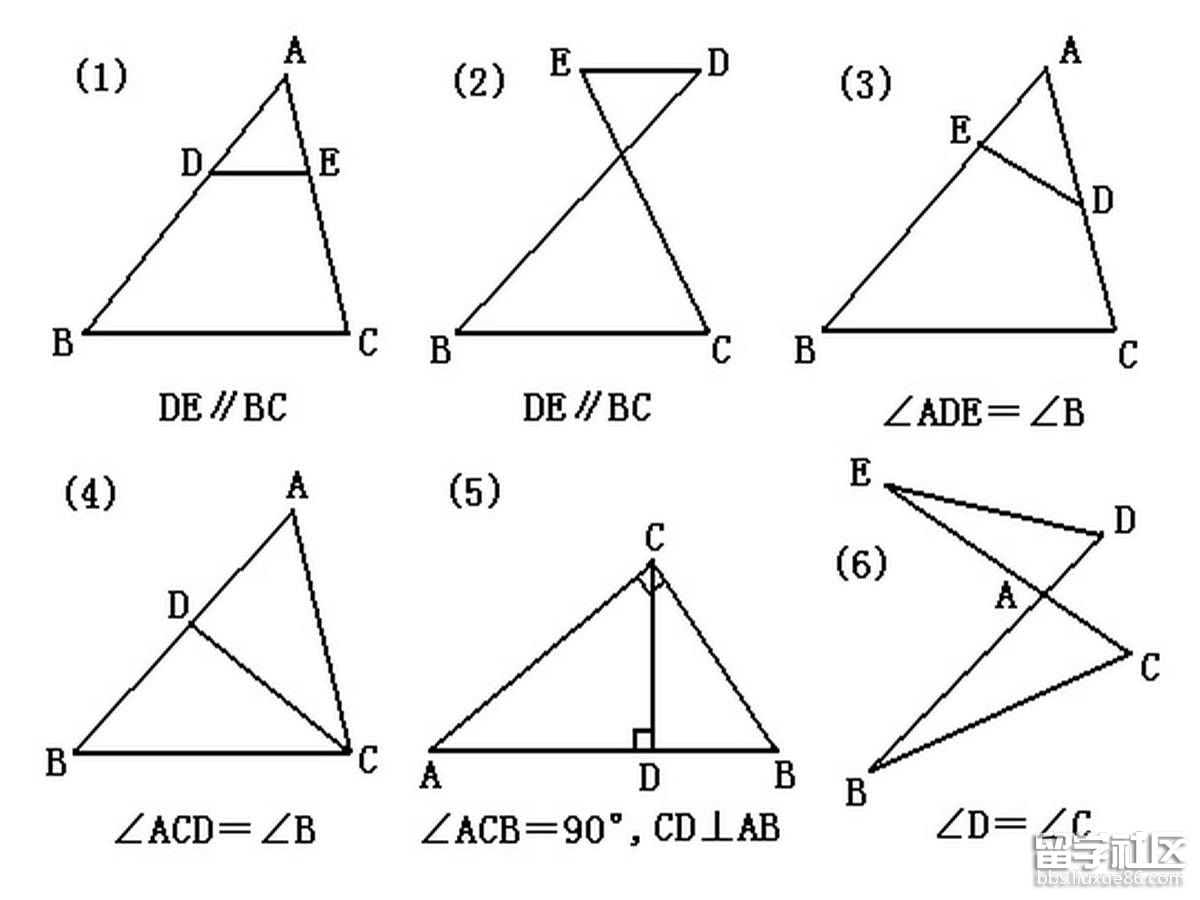
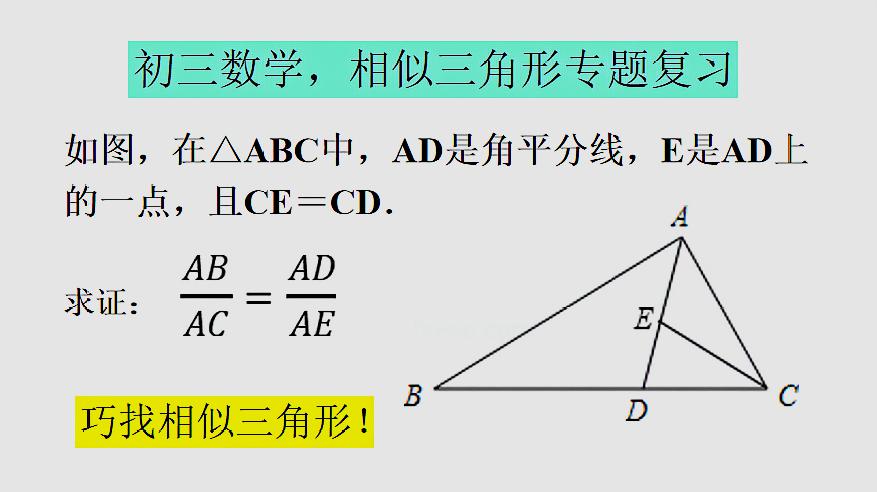
中3数学「角の二等分線定理・中点連結定理」の問題 どこよりも簡単な解き方・求め方 前回「平行線と線分の比」について学習しました この考え方と、その前に学習した「相似」を 相似は、2つの図形の形がまったく同じであれば 何倍に拡大・縮小されていても相似 ですし 回転・反転していても相似 となります。 また、「相似」かつ「大きさも同じ(1倍)」のと
Incoming Term: 数学 相似, 数学 相似符号, 数学相似形, 数学 相似条件, 数学 相似比, 数学 相似 公式, 数学 相似 中3, 数学 相似 中学, 数学 相似 合同, 数学 相似 コツ,
コメント
コメントを投稿